Guide: Regressionsdiagnostik – heteroskedasticitet, del 2

Detta är del två av vår genomgång av heteroskedasticitet. Om du vill veta mer om vad detta är och varför det kan innebära ett problem för din regression, gå genast tillbaka till del ett.

I denna andra del kommer vi att statistiskt pröva hypotesen om dess närvaro genom ett så kallat Breusch-Pagantest. Det finns en rad liknande test, men fördelen med BP-testet är att det är (relativt) enkelt att genomföra manuellt. Nackdelen är att det enbart testar närvaron av linjär heteroskedasticitet, och inte exempelvis den timglasformade varianten.

I korta ordalag går BP-testet ut på att vi, efter att ha kört den ursprungliga regressionen, gör ytterligare en, där vi testar effekten av det predicerade värdet på den beroende variabeln på (de kvadrerade) residualerna. Homoskedasticitet innebär ju jämn spridning av residualerna. Om residualerna signifikant ökar eller minskar i takt med det predicerade värdet på den oberoende variabeln har vi fog för att hävda heteroskedasticitet.

Vår modell

Data från detta övningsexempel kommer från QoGs Standard dataset (som du kan ladda ner via www.goq.gu.se/data/datadownloads). Vi är nyfikna på hur graden av korruption påverkar mänskligt välstånd i världen. Således använder vi oss av Transparency internationals mått på korruption (ti_cpi) och UNDPs mått Human Development Index (undp_hdi). Då vi tror att korruptionseffekten avtar vid lägre grad av korruption och därmed är kurvilinjär logaritmerar vi ti_cpi och skapar en ny variabel, logcpi (en guide till detta hittar du här).

Vid en första titt på förhållandet blir vi genast misstänksamma; variationen ser betydligt större ut i länder med en hög grad av korruption (Notera att ti_cpi är konstruerat så att lägre värden innebär mer korrution!). Vi är dock inte helt säkra på om detta är ett statistiskt signifikant problem eller om vi eventuellt kan strunta i det.

Nu tar vi fram papper, penna och miniräknare och ser efter.

Breusch-Pagantestet

Steg 1

Vi börjar med vår ursprungliga regression. Gå till ANALYZE -> REGRESSION -> LINEAR med undp_hdi som beroende och logcpi som oberoende variabel. Klicka på ’Save’ och fyll i att du vill spara Unstandardized Predicted Variables samt Unstandardized Residuals (dessa sparas nu i ditt dataset som nya variabler, PRE_1 och RES_1).

Kör regressionen.

Härifrån vill vi ha två saker: N-talet och Residual Sum of Squares (RSS, detta hittar vi under ANOVA-rutan i outputen). Kom ihåg dessa värden (i vårt fall är N=178 och RSS=2,457)

Steg 2

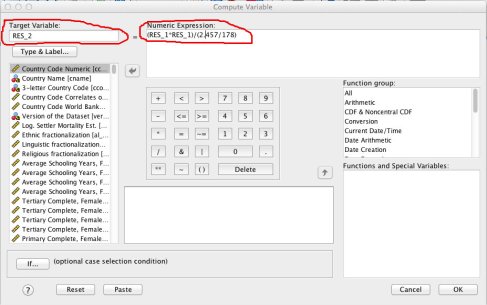
Innan vi kan genomföra själva testet måste vi först fixa till våra residualer (RES_1). Gå in på TRANSFORM -> COMPUTE VARIABLE. Vad vi vill göra är att kvadrera residualen samt standardisera den så att medelvärdet är lika med 1. Under ’Numeric Expression’ skriver vi in vår formel. Vi kvadrerar RES1 genom att multiplicera det med sig självt. Sedan dividerar vi detta med den genomsnittliga Sum of Squares. I vårt fall blir formeln som följer:

(RES_1*RES_1)/(2.457/178)

Under ’Target variable’ döper vi vår nya variabel RES_2. Tryck på OK.

Om vi vill kontrollera att variabeln är korrekt konstruerad kan vi gå in på ANALYZE -> DESCRIPTIVES, välja RES_2, och se efter så att medelvärdet är 1 (ibland kan uträkningen göra att det hamnar på något väldigt nära, typ 1,001. Det är inget problem).

Steg tre

Nu kör vi en ny regression, denna gång med RES_2 som beroende och PRE_1 som oberoende (vi kan passa på att klicka bort det vi valde att spara i steg ett under Save). Kör regressionen. Här vill vi åt Regression Sum of Squares (i vårt fall 33,106). Dividera detta värde med 2. Detta är vårt BP-värde (16,553). Skriv upp det.

Steg fyra

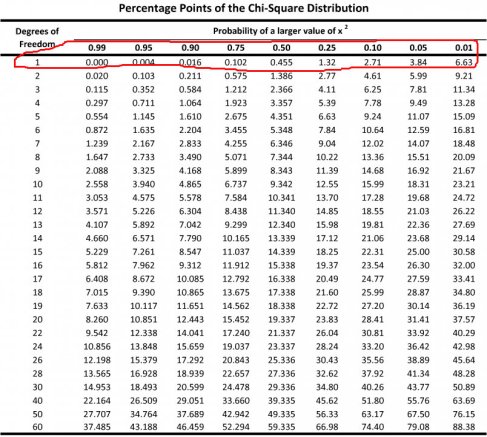
Äntligen dags för själva testet! I detta, sista, steg testar vi signifikansen på heteroskedasticiteten. Det enda vi behöver är vårt BP-värde samt en chi²-tabell, vilken du hittar i din statistikhandbok (eller här nedan).  Testet bygger på en frihetsgrad på 1. Som tabellen visar innebär ett värde på över 3,84 en 95 procents signifikant heteroskedasticitet och 2,71 en 90 procents signifikant heteroskedasticitet. Vårt värde på 16,553 är således långt över. Vi har heteroskedasticitet i vår modell…

***

En sista påminnelse som jag skrev om redan i förra delen: heteroskedasticitet bör inte enbart ses som ett problem, utan minst lika mycket som ett tecken på att ditt modellbyggande kan förbättras. Titta närmare på hur förhållandet mellan beroende och oberoende variabler ser ut – vilka fall passar bättre kring regressionskoefficienten och vilka passar sämre? Vad säger teorin?

Testet ovan har vi ju gjort på en bivariat regression men BP-testet går även bra att använda på multivariata regressioner. Gör vi om testet, men kontrollerar för logaritmerad BNP/capita (wdi_gdpc) blir heteroskedasticiteten insignifikant. Detta visar på hur heteroskedasticitet kan fungera som en kanariefågel för hur sofistikerad vår modell är och hur väl den stämmer in på verkligheten.